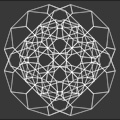
Girih Extended: The Girih Extended designs are based on scaled sets of polygons and girih tiles, a medieval Islamic patterning system. I had previously created a technique for building patterns from polygons using scaling to vary density. I then applied the technique to girih patterns, extending the original girih polygon set.

Nine hundred years ago Islamic architects developed the remarkable patterning system now known as girih, from the Persian word for “knot”. Girih are decorated polygons, aligned edge-to-edge like a tiling.

Islamic architects used girih to create intricate geometric designs from a set of five polygons. The girih system was just one of many methods used to create Islamic patterns, but it introduced an ingenious systematic approach and a departure from drafting with straightedge and compass.

My extended girih designs are made possible by adding scaling polygons to the five original girih polygons. Self-similarity and asymmetry played prominent roles in the development of this technique.

Girih Patterns: Tessellations (shapes aligned edge-to-edge with no gaps and no overlaps) can form an underlying structure for generating patterns. This makes it possible to hide the structural shapes, revealing just the pattern. An anonymous Islamic architect/mathematician masterfully created one such system, the girih tiles, allowing architects to develop elaborate patterns from just five polygons.

Islamic architects began using the girih system around 1200 CE, but the technique was lost sometime after the 15th century. The girih tile system was rediscovered in 2005 by Dr. Peter J. Lu of the Harvard University Physics Department.

In their article about girih tiles, published in the journal Science in 2007, Peter J. Lu and Paul J. Steinhardt note: “The conventional view holds that girih (geometric star-and-polygon) patterns in medieval Islamic architecture were conceived by their designers as a network of zigzagging lines, where the lines were drafted directly with a straightedge and a compass. We show that by 1200 C.E. a conceptual breakthrough occurred in which girih patterns were reconceived as tessellations of a special set of equilateral polygons (girih tiles) decorated with lines.”

Asymmetry: My extended girih system evolved from explorations of tessellations, asymmetry, lattice systems, and self-similarity. The first step in this process was simply drawing with finite polygon sets, often asymmetrically. Before adapting this system to girih, I was generating dot patterns from tessellations.

Tessellations in Islamic architecture and elsewhere are traditionally symmetrical. It’s possible, however, to arrange polygons asymmetrically without gaps or overlaps. Asymmetric patterns can be more varied and unpredictable.

Patterns made from asymmetric tessellations are interesting, but still have the overall regularity of a tiling. I wanted to vary pattern density and scale, like in drawing or engraving where the form and tone are controlled with stippling. The concept of self-similarity suggested a solution.

Scaling: Self-similar systems have parts that are identical or analogous to the whole. A seamless scaling system, though not necessarily self-similar, combines progressively sized polygons within the same tessellation. In this system smaller polygons are not similar to the whole tessellation, just similar to larger polygons within the tessellation.

Applying scaling to tessellations turned out to be the way to vary pattern density or tone. Scaling polygons are not equilateral. One side is aligned edge-to-edge with equilateral prototiles, and the other side with scaled similar polygons. The polygons are finite in shape but duplicated at progressively smaller scales. Areas with small polygons can be dense and compact, creating dark tones. Areas with larger polygons are light and open.

The five original girih tiles are a regular pentagon, a regular decagon, and three equilateral polygons—a rhombus, an elongated hexagon, and a concave hexagonal bow tie. My extended girih includes the original five polygons along with scaling polygons: kite shapes, trapezoids, or concave hexagons. I also added a second rhombus. This extended girih system creates designs reminiscent of Islamic architectural decoration, but with greater variety in pattern.

Arabesque: Girih patterns are composed of straight lines. The girih lines continue uninterrupted across polygon boundaries, and terminate at intersections within the polygons. This means that they are ideally suited for a conversion to arabesque using Bézier curves.

Where arabesque girih lines cross polygon boundaries the curves are tangent, creating a continuous flow of line. Girih boundary points define quadratic Bézier curve end points, and girih interior points become Bézier curve control points. Consequently this might be described as geometric arabesque. There's no attempt to mimic foliage. The polygons and girih patterns are used to generate the curvilinear forms.

This technique of converting girih patterns to arabesque could be applied to the basic five girih polygons. I’ve applied it to my extended girih designs. As far as I know, this is the first application of arabesque to girih tilings.

Drawing with Polygons: There’s no simple or recursive definition at work in these designs. After settling on a general goal, the solution is found through trial and error. Though digital tools were used and custom programs were developed, this is not a programmatic approach to drawing. It is still drawing with polygons.

This is design simultaneously by system and by composition. Density variation is composed by selection, and imposed by the system. The overall shape may be predetermined, but arranging polygons within it is often like solving a puzzle, not composing a design.

Girih Seven: Girih tiles have interior angles that are multiples of π/5. I’ve applied the girih concept to tiles with angles that are multiples of π/7.

Like girih tiles these have interior decoration (strapwork) that make a pattern without the polygon edges. The girih seven polygon set includes a heptagon, tetradecagon, elongated hexagon, rhombus, and bow tie. I’ve added a second rhombus, another elongated hexagon, and several scaling tiles, including a trapezoid and kites.

Transform: The Transform animations morph one 3D grid to another. Bitmap images are condensed into grids of cells. Each translucent, monochrome cell is moved forward or back based on its value. As one grid fades out another fades in.

Six Degrees of Freedom: Six Degrees of Freedom generates symmetrical patterns from perspective renderings of overlapping and rotating polyhedra. These wireframe forms, built and animated with code, endlessly rotate in shared digital space.

In each of seven segments four wireframe forms revolve around their center points. The faces of the forms include all the same polygons that are included in girih tiles.